二維碼又稱QR Code，QR全稱Quick Response，是一個近幾年來移動設備上超流行的一種編碼方式，它比傳統(tǒng)的Bar Code條形碼能存更多的信息，也能表示更多的數(shù)據(jù)類型：比如：字符，數(shù)字，日文，中文等等。這兩天學習了一下二維碼圖片生成的相關細節(jié)，覺得這個玩意就是一個密碼算法，在此寫一這篇文章 ，揭露一下。供好學的人一同學習之。
基礎知識
首先，我們先說一下二維碼一共有40個尺寸。官方叫版本Version。Version 1是21 x 21的矩陣，Version 2是 25 x 25的矩陣，Version 3是29的尺寸，每增加一個version，就會增加4的尺寸，公式是：(V-1)*4 + 21（V是版本號） 最高Version 40，(40-1)*4+21 = 177，所以最高是177 x 177 的正方形。
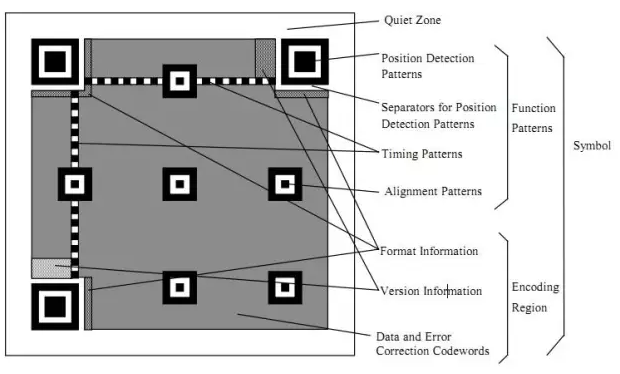
下面我們看看一個二維碼的樣例：
定位圖案
Position Detection Pattern是定位圖案，用于標記二維碼的矩形大小。這三個定位圖案有白邊叫Separators for Postion Detection Patterns。之所以三個而不是四個意思就是三個就可以標識一個矩形了。
Timing Patterns也是用于定位的。原因是二維碼有40種尺寸，尺寸過大了后需要有根標準線，不然掃描的時候可能會掃歪了。
Alignment Patterns 只有Version 2以上（包括Version2）的二維碼需要這個東東，同樣是為了定位用的。
功能性數(shù)據(jù)
Format Information 存在于所有的尺寸中，用于存放一些格式化數(shù)據(jù)的。
Version Information 在 >= Version 7以上，需要預留兩塊3 x 6的區(qū)域存放一些版本信息。
數(shù)據(jù)碼和糾錯碼
除了上述的那些地方，剩下的地方存放 Data Code 數(shù)據(jù)碼 和 Error Correction Code 糾錯碼。
數(shù)據(jù)編碼
我們先來說說數(shù)據(jù)編碼。QR碼支持如下的編碼：
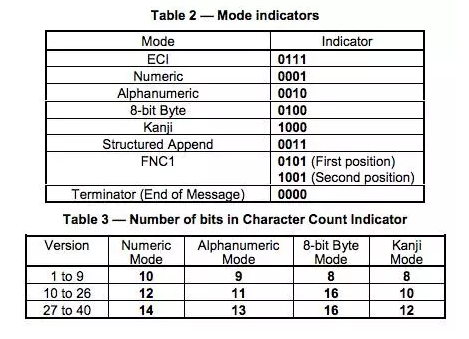
Numeric mode數(shù)字編碼，從0到9。如果需要編碼的數(shù)字的個數(shù)不是3的倍數(shù)，那么，最后剩下的1或2位數(shù)會被轉(zhuǎn)成4或7bits，則其它的每3位數(shù)字會被編成 10，12，14bits，編成多長還要看二維碼的尺寸（下面有一個表Table 3說明了這點）
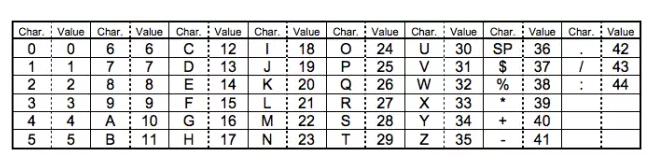
Alphanumeric mode字符編碼。包括 0-9，大寫的A到Z（沒有小寫），以及符號$ % * + – . / : 包括空格。這些字符會映射成一個字符索引表。如下所示：（其中的SP是空格，Char是字符，Value是其索引值） 編碼的過程是把字符兩兩分組，然后轉(zhuǎn)成下表的45進制，然后轉(zhuǎn)成11bits的二進制，如果最后有一個落單的，那就轉(zhuǎn)成6bits的二進制。而編碼模式和 字符的個數(shù)需要根據(jù)不同的Version尺寸編成9, 11或13個二進制（如下表中Table 3）
Byte mode, 字節(jié)編碼，可以是0-255的ISO-8859-1字符。有些二維碼的掃描器可以自動檢測是否是UTF-8的編碼。
Kanji mode這是日文編碼，也是雙字節(jié)編碼。同樣，也可以用于中文編碼。日文和漢字的編碼會減去一個值。如：在0X8140 to 0X9FFC中的字符會減去8140，在0XE040到0XEBBF中的字符要減去0XC140，然后把結果前兩個16進制位拿出來乘以0XC0，然后再 加上后兩個16進制位，最后轉(zhuǎn)成13bit的編碼。
如下圖示例：
Extended Channel Interpretation (ECI) mode主要用于特殊的字符集。并不是所有的掃描器都支持這種編碼。
Structured Append mode用于混合編碼，也就是說，這個二維碼中包含了多種編碼格式。
FNC1 mode這種編碼方式主要是給一些特殊的工業(yè)或行業(yè)用的。比如GS1條形碼之類的。
簡單起見，后面三種不會在本文中討論。
下面兩張表中，
Table 2 是各個編碼格式的“編號”，這個東西要寫在Format Information中。注：中文是1101
Table 3 表示了，不同版本（尺寸）的二維碼，對于，數(shù)字，字符，字節(jié)和Kanji模式下，對于單個編碼的2進制的位數(shù)。（在二維碼的規(guī)格說明書中，有各種各樣的編碼規(guī)范表，后面還會提到）
下面我們看幾個示例，
示例一：數(shù)字編碼
在Version 1的尺寸下，糾錯級別為H的情況下，編碼： 01234567
1. 把上述數(shù)字分成三組: 012 345 67
2. 把他們轉(zhuǎn)成二進制: 012 轉(zhuǎn)成 0000001100； 345 轉(zhuǎn)成 0101011001； 67 轉(zhuǎn)成 1000011。
3. 把這三個二進制串起來: 0000001100 0101011001 1000011
4. 把數(shù)字的個數(shù)轉(zhuǎn)成二進制 (version 1-H是10 bits ):8個數(shù)字的二進制是 0000001000
5. 把數(shù)字編碼的標志0001和第4步的編碼加到前面: 0001 0000001000 0000001100 0101011001 1000011
示例二：字符編碼
在Version 1的尺寸下，糾錯級別為H的情況下，編碼: AC-42
1. 從字符索引表中找到 AC-42 這五個字條的索引 (10,12,41,4,2)
2. 兩兩分組: (10,12) (41,4) (2)
3.把每一組轉(zhuǎn)成11bits的二進制:
(10,12) 10*45+12 等于 462 轉(zhuǎn)成 00111001110
(41,4) 41*45+4 等于 1849 轉(zhuǎn)成 11100111001
(2) 等于 2 轉(zhuǎn)成 000010
4. 把這些二進制連接起來：00111001110 11100111001 000010
5. 把字符的個數(shù)轉(zhuǎn)成二進制 (Version 1-H為9 bits ):5個字符，5轉(zhuǎn)成 000000101
6. 在頭上加上編碼標識 0010 和第5步的個數(shù)編碼: 0010 000000101 00111001110 11100111001 000010
結束符和補齊符
假如我們有個HELLO WORLD的字符串要編碼，根據(jù)上面的示例二，我們可以得到下面的編碼，
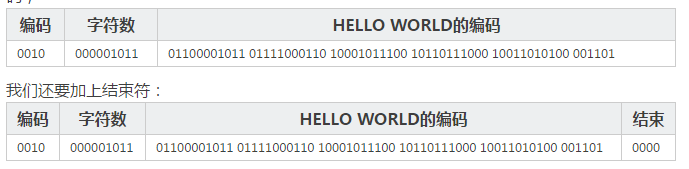
按8bits重排
如果所有的編碼加起來不是8個倍數(shù)我們還要在后面加上足夠的0，比如上面一共有78個bits，所以，我們還要加上2個0，然后按8個bits分好組：
00100000 01011011 00001011 01111000 11010001 01110010 11011100 01001101 01000011 01000000
補齊碼（Padding Bytes）
最后，如果如果還沒有達到我們最大的bits數(shù)的限制，我們還要加一些補齊碼（Padding Bytes），Padding Bytes就是重復下面的兩個bytes：11101100 00010001 （這兩個二進制轉(zhuǎn)成十進制是236和17，我也不知道為什么，只知道Spec上是這么寫的）關于每一個Version的每一種糾錯級別的最大Bits限 制，可以參看QR Code Spec的第28頁到32頁的Table-7一表。
假設我們需要編碼的是Version 1的Q糾錯級，那么，其最大需要104個bits，而我們上面只有80個bits，所以，還需要補24個bits，也就是需要3個Padding Bytes，我們就添加三個，于是得到下面的編碼：
00100000 01011011 00001011 01111000 11010001 01110010 11011100 01001101 01000011 0100000011101100 00010001 11101100
上面的編碼就是數(shù)據(jù)碼了，叫Data Codewords，每一個8bits叫一個codeword，我們還要對這些數(shù)據(jù)碼加上糾錯信息。
糾錯碼
上面我們說到了一些糾錯級別，Error Correction Code Level，二維碼中有四種級別的糾錯，這就是為什么二維碼有殘缺還能掃出來，也就是為什么有人在二維碼的中心位置加入圖標。
錯誤修正容量
L水平 7%的字碼可被修正
M水平 15%的字碼可被修正
Q水平 25%的字碼可被修正
H水平 30%的字碼可被修正
那 么，QR是怎么對數(shù)據(jù)碼加上糾錯碼的？首先，我們需要對數(shù)據(jù)碼進行分組，也就是分成不同的Block，然后對各個Block進行糾錯編碼，對于如何分組， 我們可以查看QR Code Spec的第33頁到44頁的Table-13到Table-22的定義表。注意最后兩列：
Number of Error Code Correction Blocks：需要分多少個塊。
Error Correction Code Per Blocks：每一個塊中的code個數(shù)，所謂的code的個數(shù)，也就是有多少個8bits的字節(jié)。
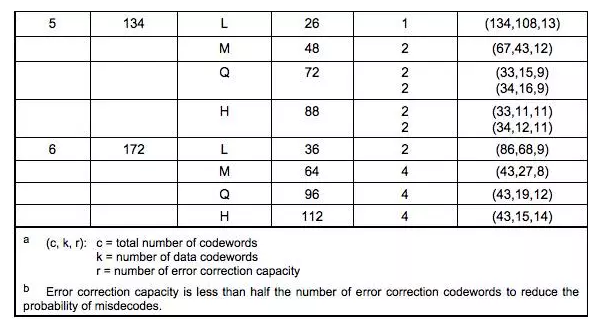
舉個例子：上述的Version 5 + Q糾錯級：需要4個Blocks（2個Blocks為一組，共兩組），頭一組的兩個Blocks中各15個bits數(shù)據(jù) + 各 9個bits的糾錯碼（注：表中的codewords就是一個8bits的byte）（再注：最后一例中的（c, k, r ）的公式為：c = k + 2 * r，因為后腳注解釋了：糾錯碼的容量小于糾錯碼的一半）
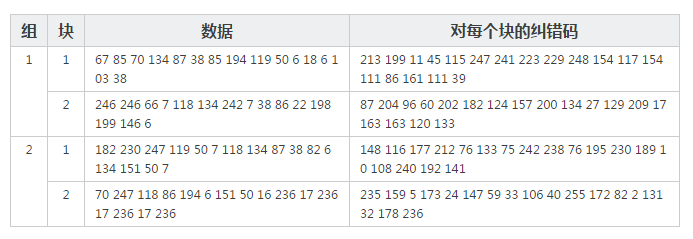
下圖給一個5-Q的示例（因為二進制寫起來會讓表格太大，所以，我都用了十進制，我們可以看到每一塊的糾錯碼有18個codewords，也就是18個8bits的二進制數(shù)）
注： 二維碼的糾錯碼主要是通過Reed-Solomon error correction（里德-所羅門糾錯算法）來實現(xiàn)的。對于這個算法，對于我來說是相當?shù)膹碗s，里面有很多的數(shù)學計算，比如：多項式除法，把1-255 的數(shù)映射成2的n次方（0<=n<=255）的伽羅瓦域Galois Field之類的神一樣的東西，以及基于這些基礎的糾錯數(shù)學公式，因為我的數(shù)據(jù)基礎差，對于我來說太過復雜，所以我一時半會兒還有點沒搞明白，還在學習 中，所以，我在這里就不展開說這些東西了。還請大家見諒了。（當然，如果有朋友很明白，也繁請教教我）
最終編碼
穿插放置
如果你以為我們可以開始畫圖，你就錯了。二維碼的混亂技術還沒有玩完，它還要把數(shù)據(jù)碼和糾錯碼的各個codewords交替放在一起。如何交替呢，規(guī)則如下：
對于數(shù)據(jù)碼：把每個塊的第一個codewords先拿出來按順度排列好，然后再取第一塊的第二個，如此類推。如：上述示例中的Data Codewords如下：
我們先取第一列的：67， 246， 182， 70
然后再取第二列的：67， 246， 182， 70， 85，246，230 ，247
如此類推：67， 246， 182， 70， 85，246，230 ，247 ……… ……… ，38，6，50，17，7，236
對于糾錯碼，也是一樣：
和數(shù)據(jù)碼取的一樣，得到：213，87，148，235，199，204，116，159，…… ……39，133，141，236
然后，再把這兩組放在一起（糾錯碼放在數(shù)據(jù)碼之后）得到：
67, 246, 182, 70, 85, 246, 230, 247, 70, 66, 247, 118, 134, 7, 119, 86, 87, 118, 50, 194, 38, 134, 7, 6, 85, 242, 118, 151, 194, 7, 134, 50, 119, 38, 87, 16, 50, 86, 38, 236, 6, 22, 82, 17, 18, 198, 6, 236, 6, 199, 134, 17, 103, 146, 151, 236, 38, 6, 50, 17, 7, 236, 213, 87, 148, 235, 199, 204, 116, 159, 11, 96, 177, 5, 45, 60, 212, 173, 115, 202, 76, 24, 247, 182, 133, 147, 241, 124, 75, 59, 223, 157, 242, 33, 229, 200, 238, 106, 248, 134, 76, 40, 154, 27, 195, 255, 117, 129, 230, 172, 154, 209, 189, 82, 111, 17, 10, 2, 86, 163, 108, 131, 161, 163, 240, 32, 111, 120, 192, 178, 39, 133, 141, 236
這就是我們的數(shù)據(jù)區(qū)。
Remainder Bits
最后再加上ReminderBits，對于某些Version的QR，上面的還不夠長度，還要加上Remainder Bits，比如：上述的5Q版的二維碼，還要加上7個bits，Remainder Bits加零就好了。關于哪些Version需要多少個Remainder bit，可以參看QR Code Spec的第15頁的Table-1的定義表。
銷售熱線：020-87030040，18924129201, 18929502661,18924129401 
微信：ivysun888/18924129201 
地址：廣東省廣州市黃埔區(qū)黃埔東路3642號豐澤高新產(chǎn)業(yè)園B棟406-410 
熱門關鍵詞：海康讀碼器,工業(yè)讀碼器,?？倒I(yè)視覺相機,OCR字符掃描槍,固定式掃描器, 
碼上關注艾韋迅
當前位置: 
